Building a decision tree from scratch
Sometimes to truly understand and internalise an algorithm, it’s always useful to build from scratch. Rather than relying on a module or library written by someone else.
I’m fortunate to be given the chance to do it in 1 of my assignments for decision trees.
From this exercise, I had to rely on my knowledge on recursion, binary trees (in-order traversal) and object oriented programming.
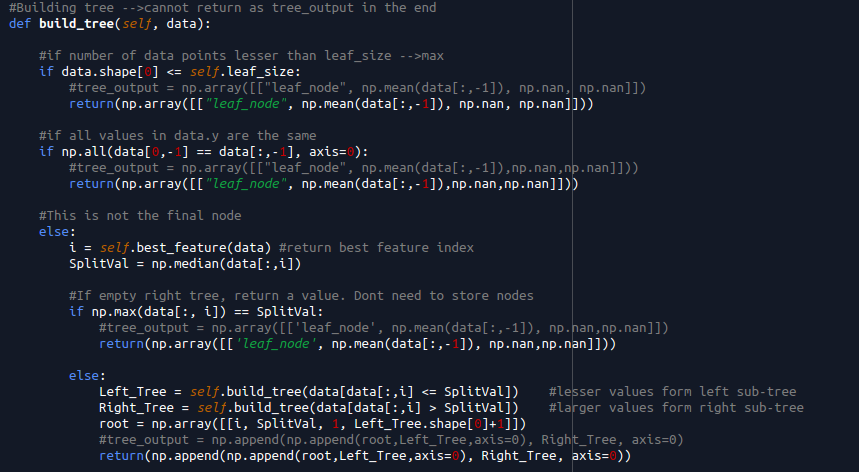
Below is a snippet of method in a class. The algorithm works as follows,
- First you define a leaf size i.e. the maximum number of data you allow to be left in the leaf node.
- If number of data in leaf node is still more than the allowable size, check if all data is the same. If it’s the same, return just 1 value
- Next I find the feature based on best correlation (gini coefficient and information gain works too) with the dependent variable values. Note that as you traverse down the tree, this dataset gets smaller
- With the best feature found in each split, I proceed to contruct the left tree and right tree together with a root node
The idea is that if you are left with a node that’s smaller or equals to allowable leaf size, it will stop traversing.