An all weather portfolio
Based on the literature, permanent portfolio is an investment strategy that is able to yield moderate returns and relatively low volatility. Investor is recommended to invest equally (25%) into GLD, Index, Bond and Cash and rebalance it back to this proportion on regular intervals.
This approach is something that I’m keen to adopt for a portion of my portfolio.
To investigate the feasibility, I simulated a portfolio starting at $300 on Nov 2004. I modified the asset allocation proportion slightly by first eliminating the cash and distributed the % amongst the following tickers,
- AGG: US Bonds
- GLD: Gold
- GSPC: SnP 500
Note:
- I admit that the code that I wrote here is very procedural. If I’ve time, I’ll try to ‘functionalize’ the codes so that I could use it for other portfolio simulation purposes.
- The looping in the R vectorized setting is known to be super slow! If I really have time to spare, I’ll convert some of the loops to Rcpp (C++). But I highly doubt so since the data is not that huge at the moment (unless I venture into tick data. Oh well, who knows).
Key points
On the annualized returns, it’s not really fantastic. But it still returns a respectable annualized performance of 5%; 1% lower than Gold and 0.5% higher than SnP 500 over the same period.
What stands out, however, are the following performance metrics:
- In terms of draw-down, it performed remarkably well relative to a pure SnP500 portfolio. It suffered a loss of only 25% as compared to a catastrophic loss of 60% duirng the financial crisis.
- On the Sharpe Ratio (annualized returns in excess of risk-free rate per unit of volatility), it’s considerably higher than GOLD and Snp500. Though it’s slightly lower than AGG.
Feel free to adapt or adopt the code. You can easily substitute the stocks based on your preferred asset allocation.
Setting up the analysis.
In this section, I downloaded stock data using quant mod. And merge the time series.
library(quantmod)## Loading required package: xts## Loading required package: zoo##
## Attaching package: 'zoo'## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric## Loading required package: TTR## Version 0.4-0 included new data defaults. See ?getSymbols.library(ggplot2)
library(PerformanceAnalytics)##
## Attaching package: 'PerformanceAnalytics'## The following object is masked from 'package:graphics':
##
## legendlibrary(tidyr)
library(dplyr)##
## Attaching package: 'dplyr'## The following objects are masked from 'package:xts':
##
## first, last## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, unionlibrary(tibble)
# Download data-->Fix the ending date for project section
ticker1 = "GLD"
stock1 = getSymbols(ticker1,from="1900-01-01",auto.assign=F)## 'getSymbols' currently uses auto.assign=TRUE by default, but will
## use auto.assign=FALSE in 0.5-0. You will still be able to use
## 'loadSymbols' to automatically load data. getOption("getSymbols.env")
## and getOption("getSymbols.auto.assign") will still be checked for
## alternate defaults.
##
## This message is shown once per session and may be disabled by setting
## options("getSymbols.warning4.0"=FALSE). See ?getSymbols for details.##
## WARNING: There have been significant changes to Yahoo Finance data.
## Please see the Warning section of '?getSymbols.yahoo' for details.
##
## This message is shown once per session and may be disabled by setting
## options("getSymbols.yahoo.warning"=FALSE).names(stock1) = c("open","high","low","close","volume","adj_close")
stock1 = stock1[,6]
ticker2 = "^GSPC"
stock2 = getSymbols(ticker2,from="1900-01-01",auto.assign=F)
names(stock2) = c("open","high","low","close","volume","adj_close")
stock2 = stock2[,6]
ticker3 = "AGG"
stock3 = getSymbols(ticker3,from="1900-01-01",auto.assign=F)
names(stock3) = c("open","high","low","close","volume","adj_close")
stock3 = stock3[,6]
# Merge the time series and subset NA
#These are the various time series
ticker_list = c("stock1","stock2","stock3")
#read in list. Loop through and assign variable to holder variable. Then assign it to combined list
ticker_all = get(ticker_list[1])
#Merging in the time series
for(i in 2:length(ticker_list)){
ticker_ind = get(ticker_list[i])
ticker_all = merge(ticker_all,ticker_ind)
}
names(ticker_all) = c("stock1","stock2","stock3")Running the simulation
Next, I run the simulation - By intialising 33% asset allocation in each of the asset and rebalance at the end of each year. Daily portfolio returns are then obtained throught the ROC function.
#Assign equal weights to each stream of returns
ticker_all = cbind(ticker_all,rowMeans(ticker_all))
ticker_all = subset(ticker_all,!is.na(ticker_all[,4]))
ticker_all = ticker_all[,-ncol(ticker_all)]
#Identify the period of rebalancing. Show the indexes
rebal_index = data.frame(index = endpoints(ticker_all,on="years")[-1])
# endpoints(ticker_all,on="quarters")
#Merge in the indicator into ticker_all--Can't seem to merge. Will do the inefficient loop
# merge(ticker_all,rebal_index, by = "index", all = T)
ticker_all$rebal = NA
for(i in 1:nrow(rebal_index)){
ticker_all$rebal[rebal_index$index[i]] = 1
}
ticker_all$rebal = ifelse(is.na(ticker_all$rebal),0,ticker_all$rebal)
#Create the returns for each price series
ticker_all$ret1 = ROC(ticker_all[,1])
ticker_all$ret2 = ROC(ticker_all[,2])
ticker_all$ret3 = ROC(ticker_all[,3])
#Initialise value for each stock series, with a total portfolio value
ticker_all$val1 = NA; ticker_all$val1[1] = 100
ticker_all$val2 = NA; ticker_all$val2[1] = 100
ticker_all$val3 = NA; ticker_all$val3[1] = 100
ticker_all$portfolio_val = NA
ticker_all$portfolio_val[1] = rowSums(ticker_all[1,8:10])
#Loop each row and 'compound'. Till it reaches the rebalancing date. Then reset stock value amount in that day. Take the portfolio value in t-1
for(i in 2:nrow(ticker_all)){
if(as.numeric(ticker_all$rebal[i]) == 0){
#During non-rebalancing days
ticker_all$val1[i] = as.numeric(ticker_all$val1[i-1]) * (1 + as.numeric(ticker_all$ret1[i]))
ticker_all$val2[i] = as.numeric(ticker_all$val2[i-1]) * (1 + as.numeric(ticker_all$ret2[i]))
ticker_all$val3[i] = as.numeric(ticker_all$val3[i-1]) * (1 + as.numeric(ticker_all$ret3[i]))
ticker_all$portfolio_val[i] = rowSums(ticker_all[i,8:10])
}else{
#During re-balancing days
ticker_all$val1[i] = ticker_all$portfolio_val[i-1] / 3
ticker_all$val2[i] = ticker_all$portfolio_val[i-1] / 3
ticker_all$val3[i] = ticker_all$portfolio_val[i-1] / 3
ticker_all$portfolio_val[i] = rowSums(ticker_all[i,8:10])
}
}
#Generate the daily portfolio returns
ticker_all$portfolio_ret = ROC(ticker_all[,11])Portfolio Performance for the entire period
On the annualized returns, it’s not really fantastic. But it still returns a respectable annualized performance of 5%; 1% lower than Gold and 0.5% higher than SnP 500 over the same period.
What stands out are the following performance metrics:
- In terms of draw-down, it performed remarkably well relative to a pure SnP500 portfolio. It suffered a loss of only 25% as compared to a loss of 60% during the financial crisis.
- On the Sharpe Ratio (annualized returns in excess of risk-free rate), it’s considerably higher than GOLD and Snp500. Though it’s slightly lower than AGG.
######################################Study the portfolio returns########################################
#Carry out the portfolio return series
table.Drawdowns(ticker_all$portfolio_ret, top=10)## From Trough To Depth Length To Trough Recovery
## 1 2008-02-29 2008-11-20 2010-05-11 -0.2597 554 186 368
## 2 2006-05-11 2006-06-14 2007-02-01 -0.1071 183 24 159
## 3 2012-10-05 2013-06-27 2014-06-30 -0.1040 434 181 253
## 4 2015-01-23 2016-01-19 2016-06-15 -0.0939 352 249 103
## 5 2011-09-06 2011-10-04 2012-02-02 -0.0702 104 21 83
## 6 2016-08-19 2016-12-15 2017-05-26 -0.0675 194 83 111
## 7 2012-02-29 2012-05-16 2012-09-07 -0.0605 134 55 79
## 8 2010-05-13 2010-07-06 2010-09-14 -0.0479 86 37 49
## 9 2018-01-29 2018-02-08 <NA> -0.0479 44 9 NA
## 10 2007-05-08 2007-08-16 2007-09-11 -0.0434 88 71 17table.DownsideRisk(merge(ticker_all$portfolio_ret, ticker_all$ret1, ticker_all$ret2, ticker_all$ret3))## portfolio_ret ret1 ret2 ret3
## Semi Deviation 0.0042 0.0087 0.0087 0.0023
## Gain Deviation 0.0037 0.0079 0.0084 0.0021
## Loss Deviation 0.0045 0.0090 0.0100 0.0026
## Downside Deviation (MAR=210%) 0.0098 0.0135 0.0134 0.0087
## Downside Deviation (Rf=0%) 0.0041 0.0085 0.0086 0.0022
## Downside Deviation (0%) 0.0041 0.0085 0.0086 0.0022
## Maximum Drawdown 0.2597 0.4922 0.6103 0.1313
## Historical VaR (95%) -0.0087 -0.0188 -0.0179 -0.0038
## Historical ES (95%) -0.0136 -0.0287 -0.0300 -0.0064
## Modified VaR (95%) -0.0091 -0.0189 -0.0177 -0.0008
## Modified ES (95%) -0.0195 -0.0341 -0.0302 -0.0008table.AnnualizedReturns(merge(ticker_all$portfolio_ret, ticker_all$ret1, ticker_all$ret2, ticker_all$ret3))## portfolio_ret ret1 ret2 ret3
## Annualized Return 0.0491 0.0620 0.0432 0.0363
## Annualized Std Dev 0.0899 0.1893 0.1885 0.0482
## Annualized Sharpe (Rf=0%) 0.5464 0.3274 0.2294 0.7535charts.PerformanceSummary(merge(ticker_all$portfolio_ret, ticker_all$ret1, ticker_all$ret2, ticker_all$ret3))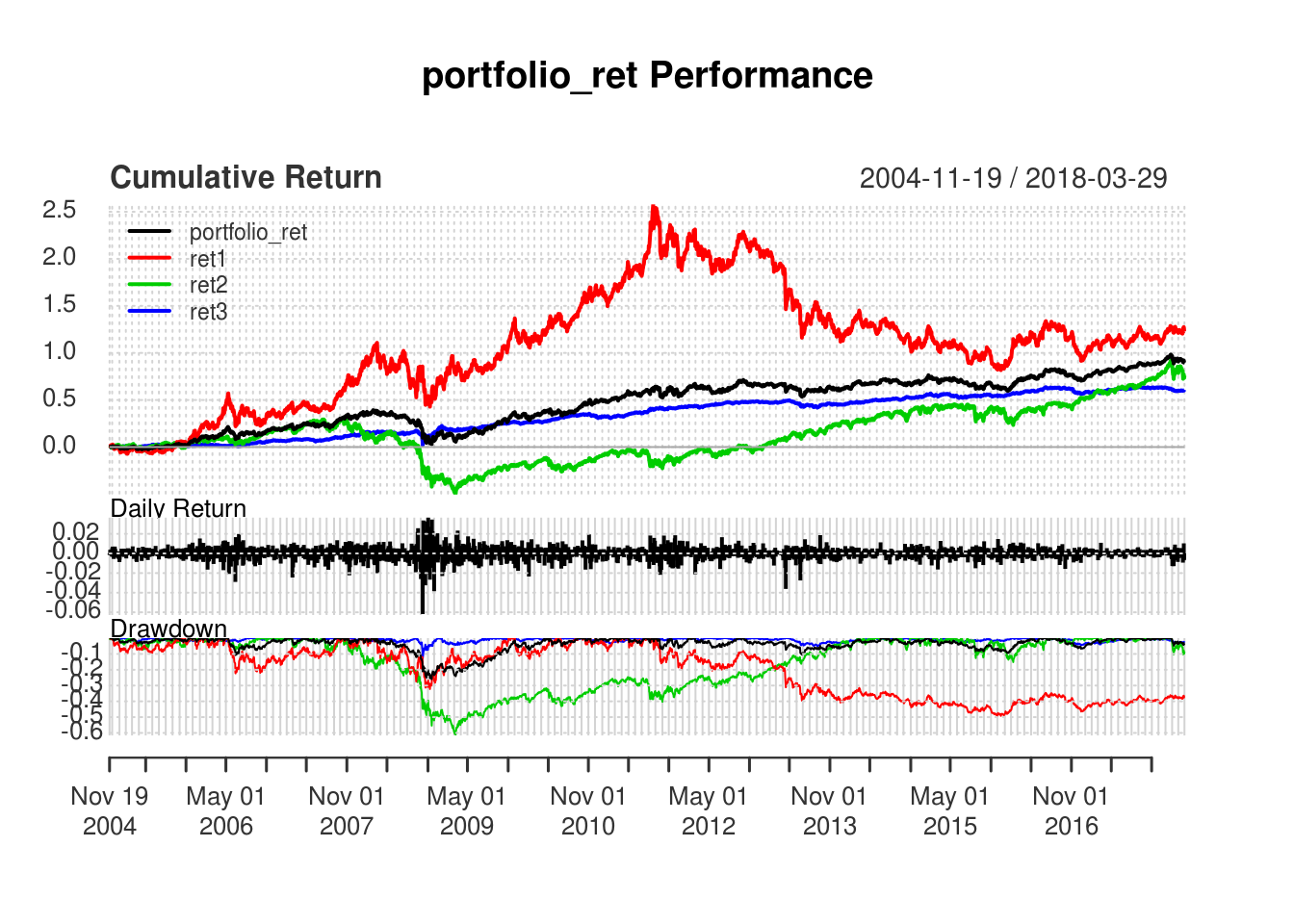
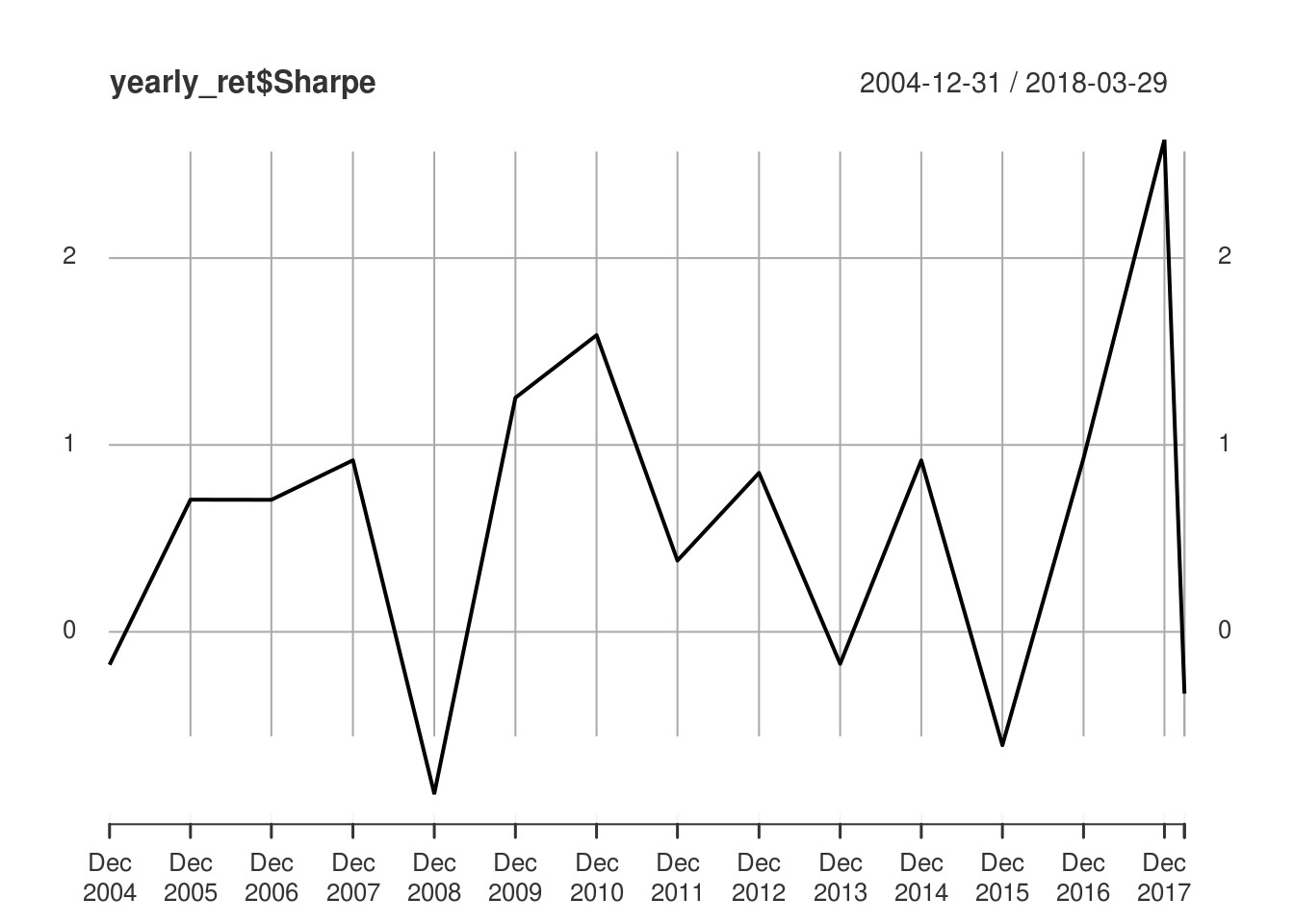
Yearly Portfolio Performance
I also tabulated the yearly metrics of the portfolio to give a sense of the performance over years.
#####################################Study the annualized portfolio returns series#######################
#Use the rebal-indicator. Loop through the chunks
# https://www.quantmod.com/documentation/periodReturn.html
# https://rpubs.com/mohammadshadan/288218
# yearly_ret = periodReturn(ticker_all$portfolio_val
# ,period='yearly',subset='2004::') # returns years 2003 to present
yearly_ret = periodReturn(ticker_all$portfolio_val
,period='yearly') # returns years 2003 to present
#Inefficient way to calulate standard deviation. If it've time, I will probably optimize this
split_val = split(ticker_all$portfolio_ret, f = "years")
yearly_ret$annual_sd = sapply(X = split_val, FUN = StdDev) * sqrt(252)
getSymbols('DGS3MO',src = 'FRED')## [1] "DGS3MO"rf = DGS3MO; rm(DGS3MO)
rf = rf["2004/2018"]
split_val_rf = split(rf$DGS3MO, f = "years")
yearly_ret$annual_rf = sapply(X = split_val_rf, FUN = mean, na.rm = T)/100
yearly_ret$Sharpe = (yearly_ret$yearly.returns - yearly_ret$annual_rf)/yearly_ret$annual_sd
yearly_ret## yearly.returns annual_sd annual_rf Sharpe
## 2004-12-31 0.004226944 0.05540773 0.0139872000 -0.1761533
## 2005-12-30 0.072086547 0.05645463 0.0321612000 0.7072112
## 2006-12-29 0.119531756 0.10051348 0.0485156000 0.7065336
## 2007-12-31 0.128879475 0.09157342 0.0448095618 0.9180602
## 2008-12-31 -0.128296533 0.16426474 0.0139685259 -0.8660718
## 2009-12-31 0.146831877 0.11599763 0.0015092000 1.2528072
## 2010-12-31 0.142566228 0.08892810 0.0013844622 1.5875945
## 2011-12-30 0.038641897 0.09995615 0.0005284000 0.3813022
## 2012-12-31 0.063250462 0.07334484 0.0008760000 0.8504275
## 2013-12-31 -0.013798292 0.08392775 0.0005708000 -0.1712079
## 2014-12-31 0.052948032 0.05736776 0.0003272000 0.9172544
## 2015-12-31 -0.041404619 0.06912477 0.0005250996 -0.6065802
## 2016-12-30 0.061886147 0.06319037 0.0031936000 0.9288211
## 2017-12-29 0.115604533 0.04028321 0.0094896000 2.6342224
## 2018-03-29 -0.010810745 0.08058259 0.0158213115 -0.3304939plot(yearly_ret$yearly.returns)
plot(yearly_ret$Sharpe)